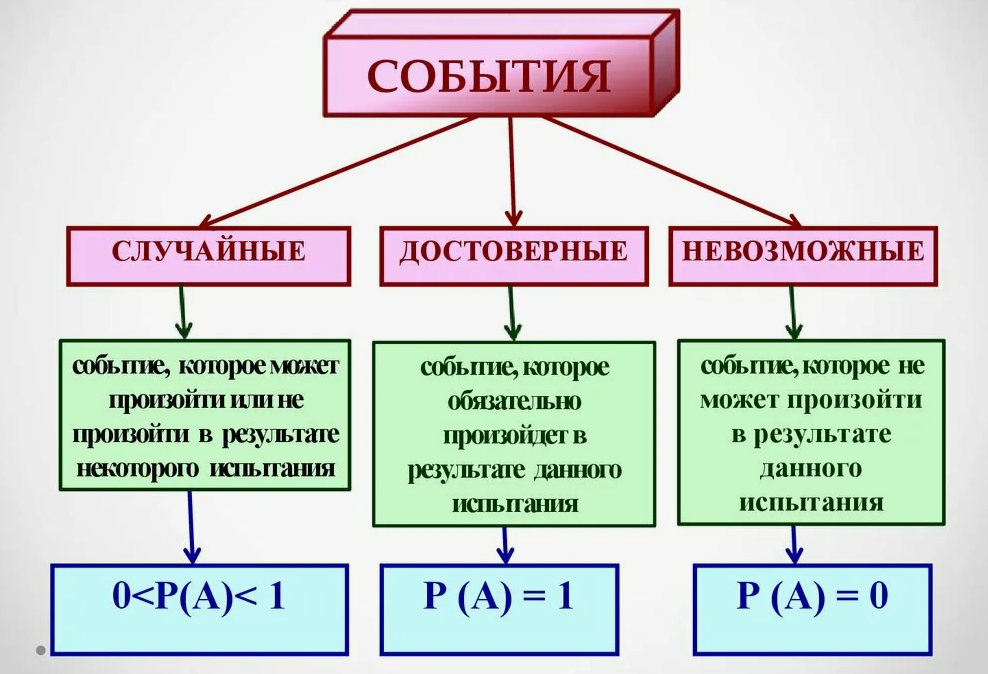
Достоверное. Событие, которое при данных условиях всегда произойдёт.
Невозможное. Событие, которое в данных условиях не может произойти.
Равновозможные. События, которые имеют одинаковые шансы наступления.
Неравновозможные. Одно из событий имеет больше возможностей, чем другие.
Несовместные. Наступление одного из событий исключает наступление других событий в одном и том же опыте.
Совместные. Наступление одного из событий не исключает наступления других событий в одном и том же опыте.
Противоположные. Одно из двух событий происходит тогда, когда не происходит другое.
Независимые. Появление одного события не зависит от появления другого.
ЭЛЕМЕНТАРНЫЕ СОБЫТИЯ. ВИДЫ СОБЫТИЙ
ЭЛЕМЕНТАРНЫЕ СОБЫТИЯ, ИХ ВЕРОЯТНОСТЬ
Вероятность достоверного события равна единице.
Вероятность невозможного события равна нулю.
Вероятность случайного события есть положительное число, заключённое между нулём и единицей.
Случайный выбор – это разновидность такого опыта, в котором элементарным событием является извлечение одного предмета из изучаемой группы.
СЛУЧАЙНЫЙ ВЫБОР
Элементарные события – это возможные, исключающие друг друга результаты испытания, которые нельзя разложить на более простые события.

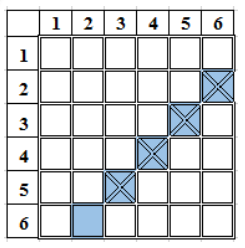

Случайно выбранная кость в игре домино оказалась не дублем.
Найти вероятность того, что вторую также взятую наудачу кость домино можно приставить к первой.
Решение:
1) n=27 - число всех оставшихся костей
2) m=6+6=12, т.к. первая кость – не дубль, к ней можно приставить 6 костей к одной половине или 6 костей к другой половине.
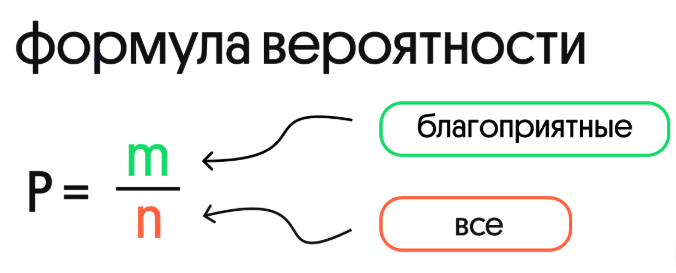
3) P=m/n, где m – число исходов, благоприятствующих осуществлению события, а n – число всех возможных элементарных исходов
P=12/27≈0,444
Ответ: 0,444.

Пятитомное собрание сочинений расположено на полке в случайном порядке.
Какова вероятность того, что книги стоят слева направо в порядке нумерации томов (от 1 до 5)?
Решение:
1) n=5!=1*2*3*4*5=120 - число различных перестановок из 5 книг на полке
2) найдем число благоприятствующих описанному в задаче событию исходов – есть только одна расстановка, когда книги стоят слева направо в порядке нумерации томов (от 1 до 5), то есть m =1
3) P=m/n, где m – число исходов, благоприятствующих осуществлению события, а n – число всех возможных элементарных исходов
P=1/120≈0,0083
Ответ: 0,0083.



