ИСПЫТАНИЕ. УСПЕХ И НЕУДАЧА.
СЕРИЯ ИСПЫТАНИЙ ДО ПЕРВОГО УСПЕХА
Серией испытаний Бернулли называют одинаковые и независимые испытания, проведённые определённое количество раз (несколько раз). Испытания не зависят друг от друга.
Элементарным событием в серии испытаний Бернулли является последовательность успехов и неудач, а не отдельный успех или неуспех.
В серии из n испытаний Бернулли всего 2n различных элементарных событий.
Формула для расчёта вероятности того, что событие A наступит ровно k раз из n, называется «формулой Бернулли»:
и успех случается впервые на каком-либо шаге испытаний. Как только успех случился, испытания прекращаются.
В испытаниях до достижения первого успеха отсутствует фиксированное количество испытаний. Победа в серии испытаний может наступить на любом из шагов.
Искомая вероятность наступления первого успеха зависит только от вероятности успеха p и от номера шага k, на котором наступит первый успех.
- Результатом каждого испытания является один из двух возможных исходов, называемых соответственно «успехом» или «неудачей».
- Вероятность «успеха» в каждом последующем испытании не зависит от результатов предыдущих испытаний и остаётся постоянной.




которое позволяет находить степень суммы двух чисел/переменных.
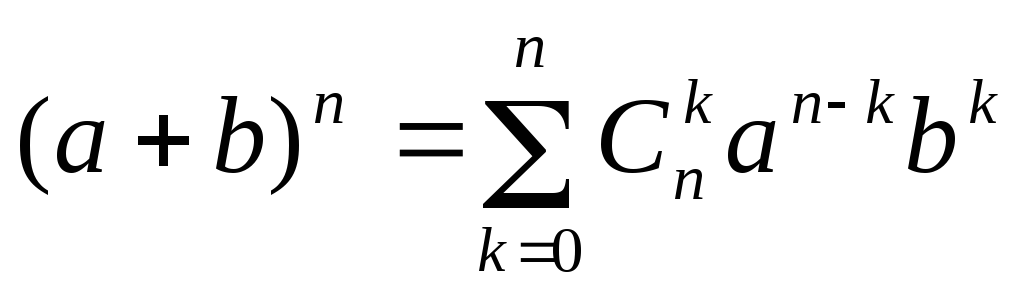
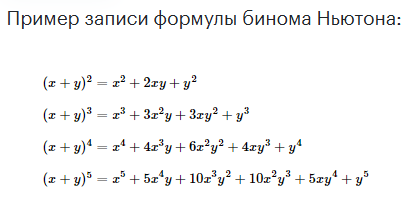
Алгоритм расчёта бинома Ньютона:
- Подставить заданные числа в формулу. Числа в скобках могут быть любыми, а степень обязательно должна быть натуральным числом, то есть целым, положительным, не равным нулю.
- Раскрыть знак суммы и выписать слагаемые.
- Упростить выражение.
- Рассчитать биномиальные коэффициенты. Они показывают, на какие числа нужно умножить каждое слагаемое в многочлене. Значения коэффициентов повторяются: первый равен последнему, а второй — четвёртому. Поэтому можно считать не все коэффициенты, а только половину (и ещё один «посередине», если степень многочлена чётная).
- Считать факториалы и сократить.
- Подставить полученные коэффициенты в формулу.

Найдите вероятность того, что выигрыш (У-удача=0,3) и проигрыш (Н-неудача=0,7) чередовались в течение недели.
Решение:
1) p(УНУНУНУ)=0,34+0,73=0,351
2) p(НУНУНУН)=0,33+0,74=0,267
Ответ: 0,351 и 0,267.

Что более вероятно выиграть у равносильного противника: не менее двух партий из трёх или не более одной из двух?
Решение:
Используем формулу Бернулли Pn(k)=Cknpkqn-k – вероятность выиграть в точности k партий из n , где p=0,5 – вероятность выигрыша, q=1-0,5=0,5 – вероятность проигрыша. Тогда Pn(k)=Ckn0,5k0,5n-k
1) не менее 2 партий из 3:
P1=P3(k>=2)=P3(2)+P3(3)=C23*0,53+C33*0,53=3*0,53+0,53= 4*0,53=0,5
2) не более 1 партии из 2:
P2=P2(k<=1)=P2(0)+P2(1)=C02*0,52+C12*0,52=3*0,52=0,75
Так как P2>P1 (0,75>0,5), второй вариант вероятнее.
Ответ: более вероятно выиграть не более одной партии из двух.



