МНОЖЕСТВА. ПОДМНОЖЕСТВО. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ
МНОЖЕСТВА
Множества в статистике используются для описания и расчёта вероятности различных событий.
Они помогают организовывать и понимать различные исходы эксперимента.
Они помогают организовывать и понимать различные исходы эксперимента.
Множество – совокупность (произвольный набор) каких-либо объектов. Объекты множества – это его элементы.
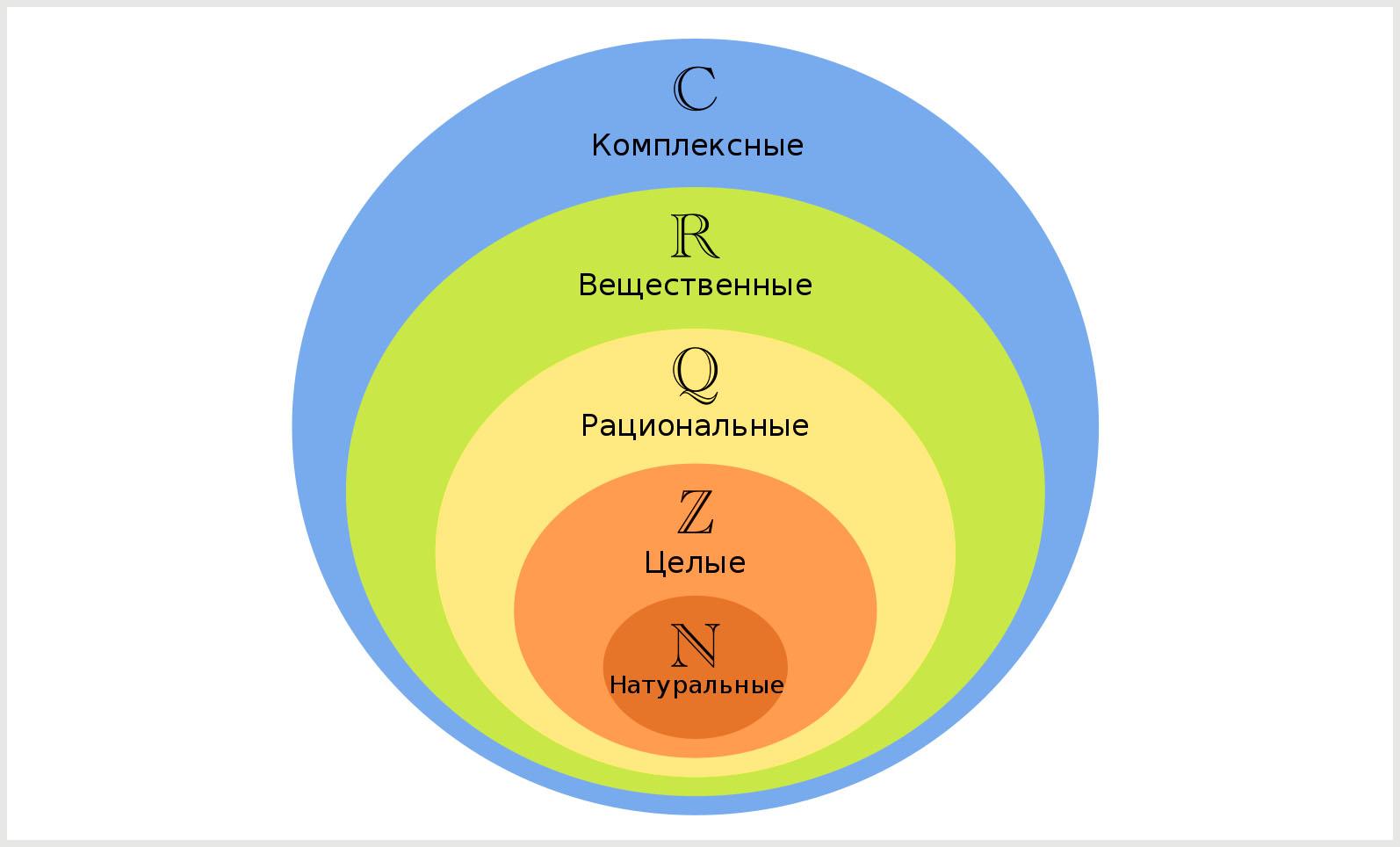
Например, это могут быть числа, цифры, точки на прямой, на плоскости или в пространстве, геометрические фигуры, события, слова, теоремы, окружающие предметы.
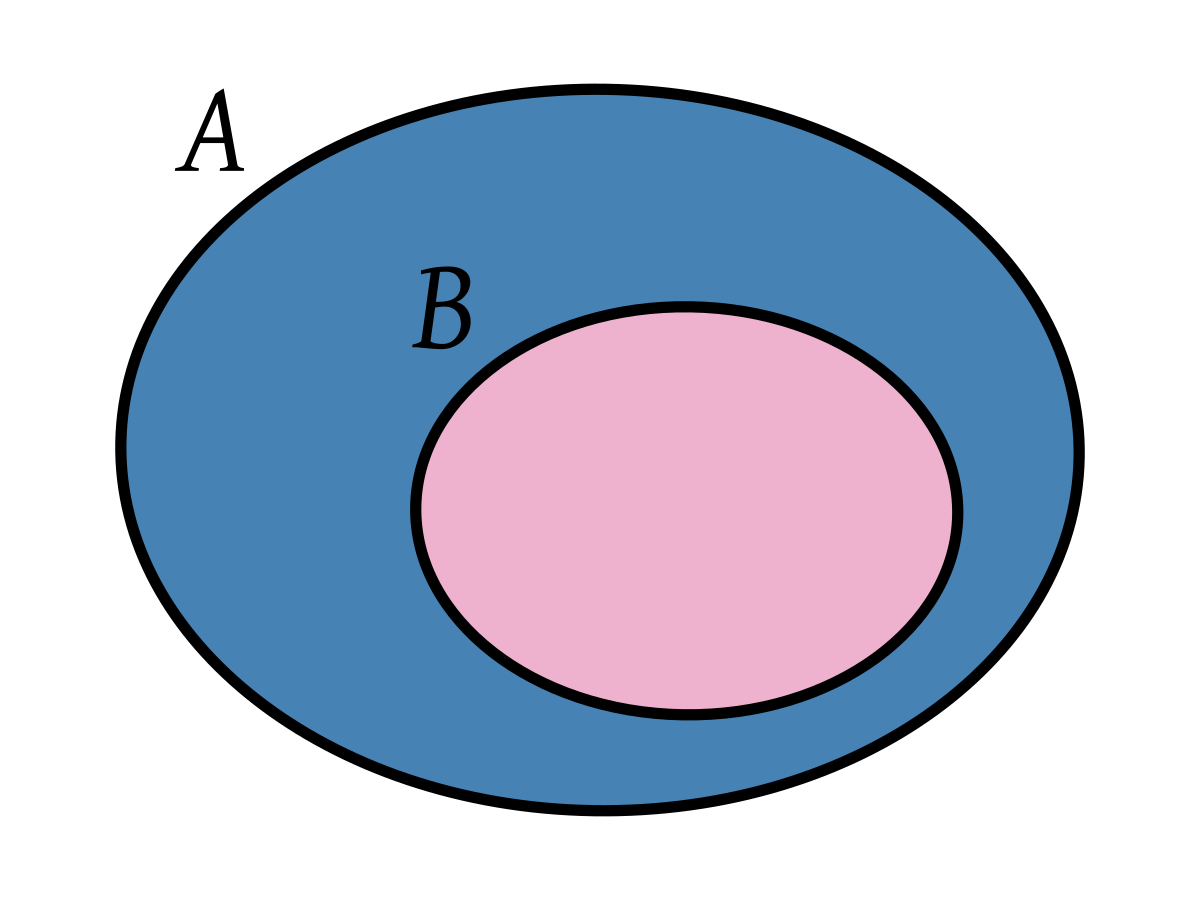
Подмножество – это часть множества, любой элемент которой также принадлежит этому множеству.
Операции над множествами позволяют получать новые множества. Операции бывают бинарные (которые выполняются над двумя множествами) и унарные (которые выполняются над одним множеством).
К основным операциям над множествами относятся:
Дополнение – множество элементов, которые не содержатся в первоначальном множестве. Под универсальным множеством понимают максимальное множество, содержащее все возможные элементы.
Пример: если к множеству растений добавить множество животных, получится универсальное множество живой природы.
Например, это могут быть числа, цифры, точки на прямой, на плоскости или в пространстве, геометрические фигуры, события, слова, теоремы, окружающие предметы.
Подмножество – это часть множества, любой элемент которой также принадлежит этому множеству.
Операции над множествами позволяют получать новые множества. Операции бывают бинарные (которые выполняются над двумя множествами) и унарные (которые выполняются над одним множеством).
К основным операциям над множествами относятся:
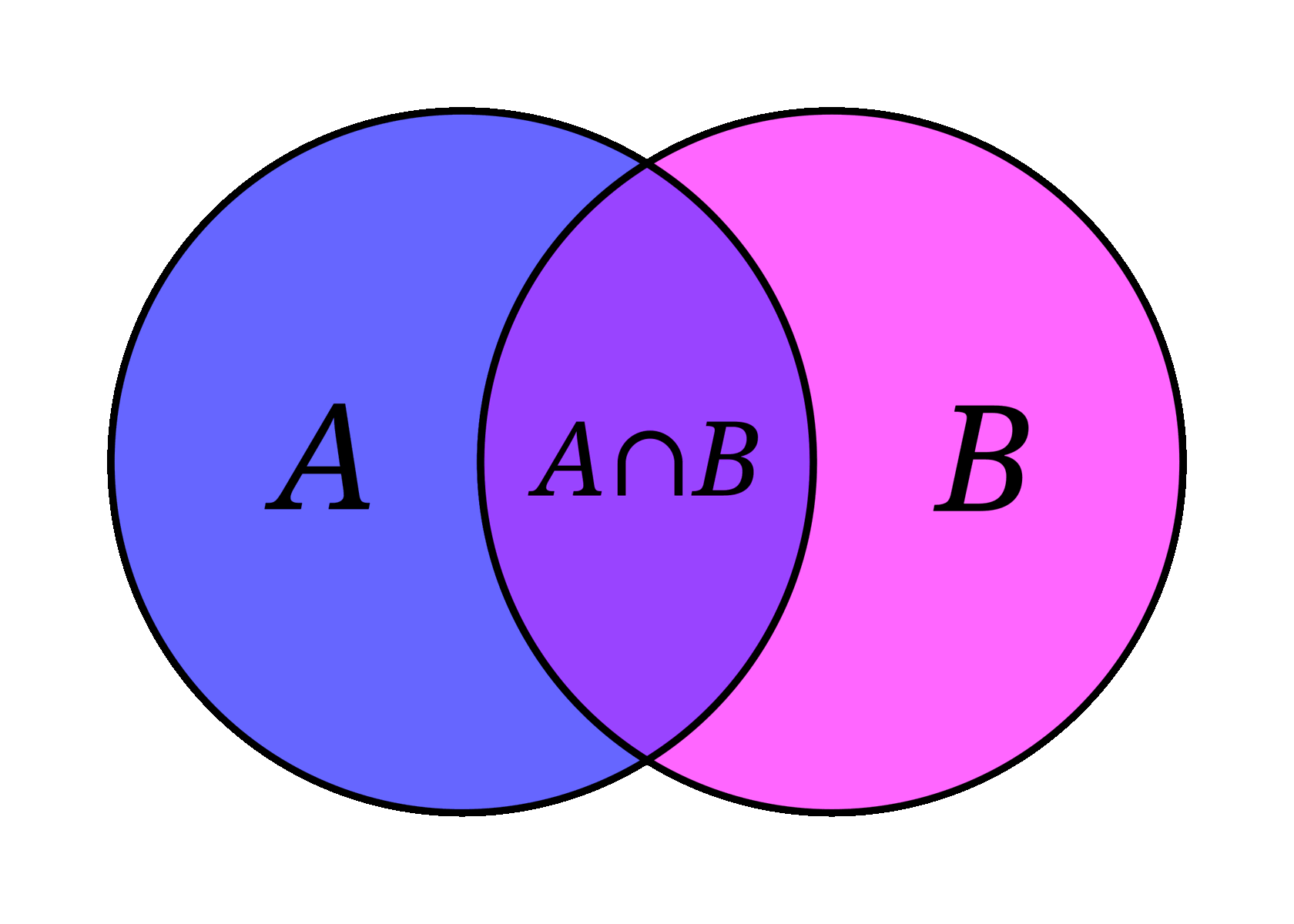
- Пересечение. Пересечение двух множеств – это множество, содержащее элементы, принадлежащие и первому множеству, и второму множеству. Пример: множество домашних животных включает в себя элементы из множества собак и множества кошек.
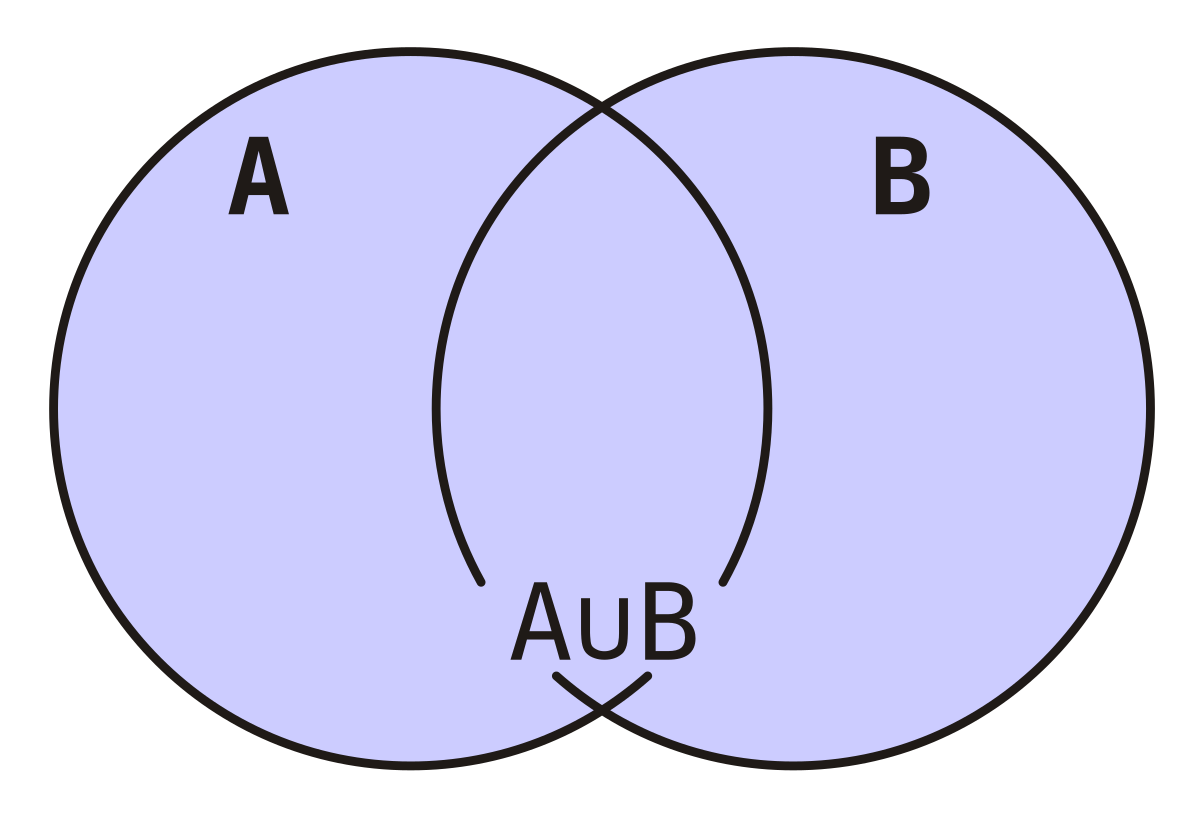
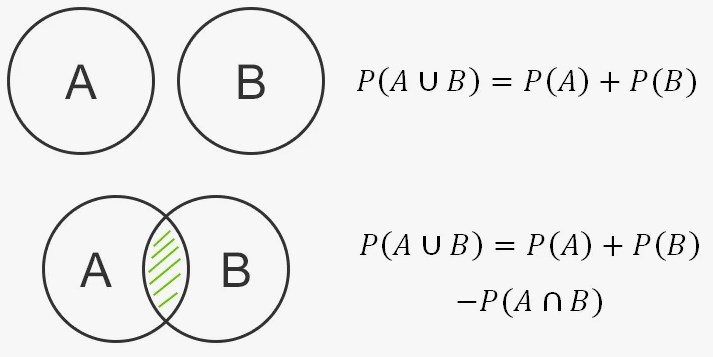
- Объединение. Объединение двух множеств – это множество, содержащее все элементы, принадлежащие хотя бы одному из первого или второго множеств. При объединении множеств общие элементы учитываются один раз. Пример: множество треугольников, множество четырёхугольников, множество замкнутых ломаных объединяются во множество многоугольников.
- Разность. Разностью двух множеств называется множество, содержащее все элементы первого множества, но не принадлежащие второму множеству. Пример: если из множества грибов исключить множество ядовитых грибов, то останется множество съедобных грибов.
Дополнение – множество элементов, которые не содержатся в первоначальном множестве. Под универсальным множеством понимают максимальное множество, содержащее все возможные элементы.
Пример: если к множеству растений добавить множество животных, получится универсальное множество живой природы.
Свойства операций над множествами:
Основные методы графического представления множеств:
- Переместительное свойство (для объединения и пересечения). Операции объединения и пересечения множеств являются переместительными.
- Сочетательное свойство (для объединения и пересечения). Операции объединения и пересечения множеств являются сочетательными.
- Распределительное свойство. Операция пересечения распределяется относительно операции объединения, и наоборот.
- Свойство включения. Если одно множество является подмножеством другого, это означает, что каждый элемент множества A принадлежит множеству B.
Основные методы графического представления множеств:
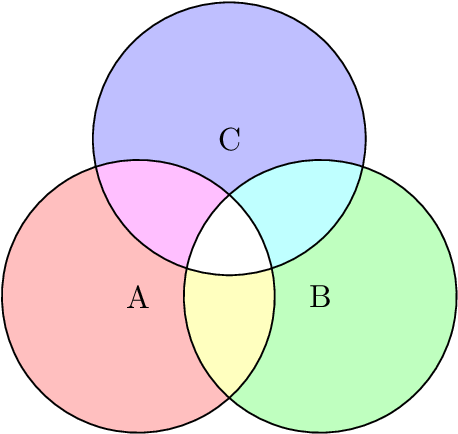
- Диаграммы Эйлера (Диаграммы Венна). Это набор пересекающихся окружностей, которые представляют элементы множества и их пересечения.
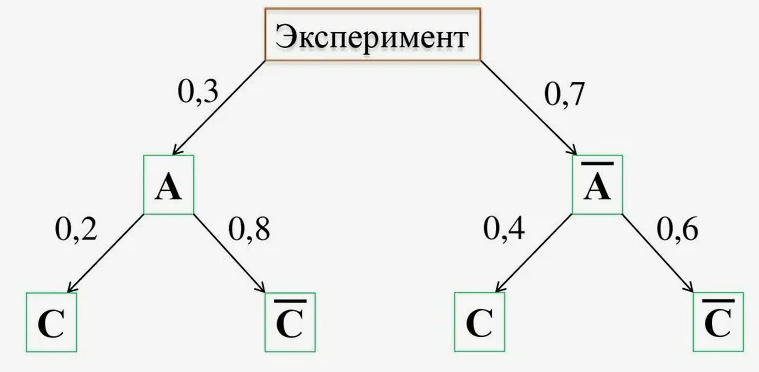
- Деревья. Это графическое представление множества, где элементы множества представлены вершинами дерева, а их отношения – рёбрами дерева.
СВОЙСТВА ОПЕРАЦИЙ НАД МНОЖЕСТВАМИ.
ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ МНОЖЕСТВ
ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ МНОЖЕСТВ
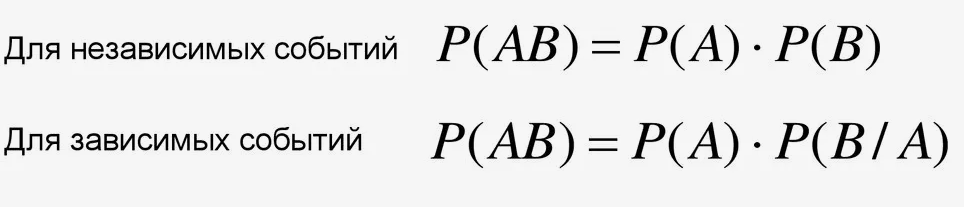
РЕШЕНИЕ ЗАДАЧ

Задача 1
В коробке 7 красных и 3 синих шара. По очереди извлекают 2 шара. Какова вероятность того, что извлекут шары разного цвета?
1) А - красный и синий (кс), В - синий и красный (кс)
2) р(А)=7/10*3/9=7/10
3) р(В)=3/10*7/9=7/30
4) p(A∪B)=p(A)+p(B)=7/15
Ответ: 7/15.

Задача 2
В городе 48% населения - мужчины, а среди мужчин 15% - пенсионеры. Найти вероятность того, что случайно выбранный житель города окажется мужчина на пенсии.
1) А={житель пенсионер}, В={житель мужчина}
2) p(A∩B)=p(В)*p(А/B)=0,48*0,15=0,072 - условная вероятность события А, при условии, что В уже наступило
Ответ: 0,072.

Решение:
1) 150+86+11=247
2) 247-41=206 9 (т.к. говорящих на двух языках мы посчитали дважды)
Ответ: 206.
1) 150+86+11=247
2) 247-41=206 9 (т.к. говорящих на двух языках мы посчитали дважды)
Ответ: 206.

Решение:
- 35 - 10 = 25 (чел) — записаны в кружки
- 20 + 11 = 31 (чел) — записаны в кружки (с учётом того, что один человек может быть записан в два кружка одновременно)
- 31 - 25 = 6 (чел) — записаны и в математический, и в биологический кружок

