Правило. Чтобы вычислить среднее арифметическое нескольких чисел, нужно взять сумму этих чисел и разделить все на количество слагаемых. Частное и будет средним арифметическим этих чисел.
Мода ряда чисел – это число, которое встречается в данном ряду чаще других.
Правило. Модой может быть как одно число, так и сразу несколько, а если ни одно числовое значение не повторяется чаще других, моды не будет совсем.
Медиана – это среднее значение в упорядоченном наборе чисел. То есть такое число набора, которое не больше ровно половины его элементов и не меньше тоже ровно половины.
Правило. Чтобы найти медиану числового набора, содержащего нечётное количество чисел, нужно упорядочить их по возрастанию, а затем найти число, находящееся ровно посередине. Для набора чисел с чётным количеством элементов нужно упорядочить их по возрастанию, затем найти два числа, находящихся в середине, и найти их среднее арифметическое, или полусумму.
Частота – это число повторений, показывающее, сколько раз за какой-то период происходило некоторое событие, проявлялось определённое свойство объекта либо наблюдаемый параметр достигал данной величины. То есть частота определяет то, как часто повторяется та или иная величина в выборке.
Частоты бывают двух видов – абсолютные и относительные:
Абсолютная частота определяет, как часто определённое событие происходит в данном эксперименте.
Относительная частота – это отношение абсолютной частоты к общему количеству. Как правило, относительная частота выражается в процентах.
ЧИСЛОВЫЕ НАБОРЫ. МЕРЫ ЦЕНТРАЛЬНОЙ ТЕНДЕНЦИИ
Наибольшее значение – это не то значение, которое больше всех остальных чисел в наборе, а то значение, которое не меньше всех других
(больше или равно).
Наименьшее значение – то, которое не больше всех других чисел.
Размах числового набора – разность между наибольшим и наименьшим значением этого числового набора. Размах равен длине отрезка, на котором располагаются все значения.
Дисперсия – среднее арифметическое квадратов отклонений чисел от их среднего арифметического.
Стандартное отклонение – квадратный корень из дисперсии этого набора.
Стандартное отклонение показывает разброс значений относительно среднего значения. Чем меньше стандартное отклонение, тем ближе значения к среднему. Чем больше стандартное отклонение, тем больше разброс данных
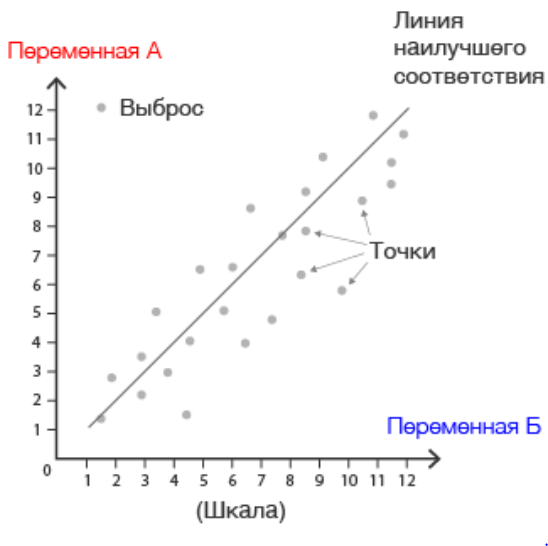
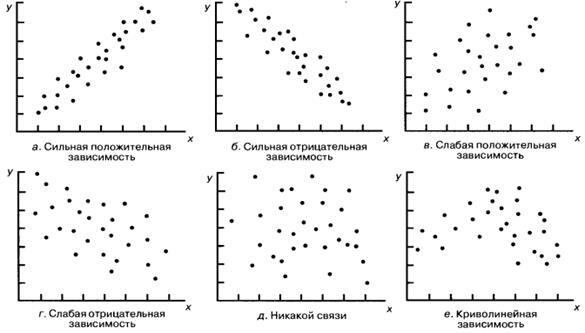
Диаграмма рассеивания – способ представления двух совместно наблюдаемых величин точками на координатной плоскости.
Данные точки образуют облако рассеивания.
С помощью диаграмм рассеивания можно определить потенциальные взаимосвязи между количественными переменными. Форма и расположение облака рассеивания позволяет выявить взаимосвязь или её отсутствие между компонентами и определить характер связи.
В простой диаграмме рассеяния используется плоская система координат для просмотра значений двух переменных. В объёмной диаграмме рассеяния – трёхмерная система координат для просмотра значений трёх переменных.
ОТКЛОНЕНИЕ. ДИСПЕРСИЯ ЧИСЛОВОГО НАБОРА
2) Если из всех значений признака отнять какое-либо постоянное число, то средняя величина из новых значений уменьшится на это же число.
3) Если ко всем значениям признака прибавить какое-либо постоянное число, то средняя величина из новых значений увеличится на это же число.
4) Если все значения признака умножить на постоянное число, то средняя величина из новых значений увеличится во столько же раз.
5) Если значения признака разделить на какое-либо постоянное число, то средняя величина из новых значений уменьшится во столько же раз.
6) Если частоты всех значений признака разделить или умножить на постоянное число, то средняя величина от этого не изменится.
7) Сумма всех отклонений отдельных значений признака от средней величины всегда равняется нулю. При вычислении сумма положительных отклонений (когда индивидуальное значение больше средней величины) будет равна сумме отрицательных отклонений (когда индивидуальное значение меньше среднего значения).
и представлением данных с целью их простого обобщения и описания.



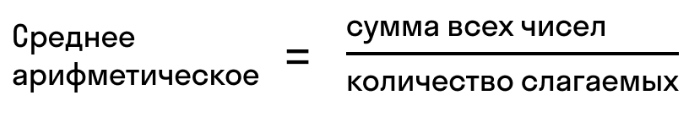


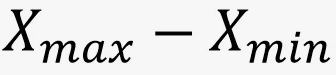
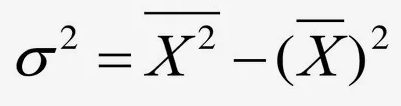
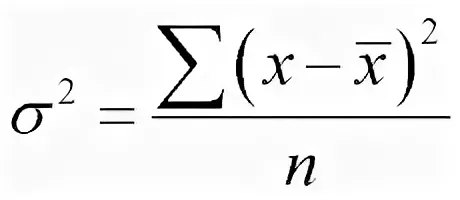
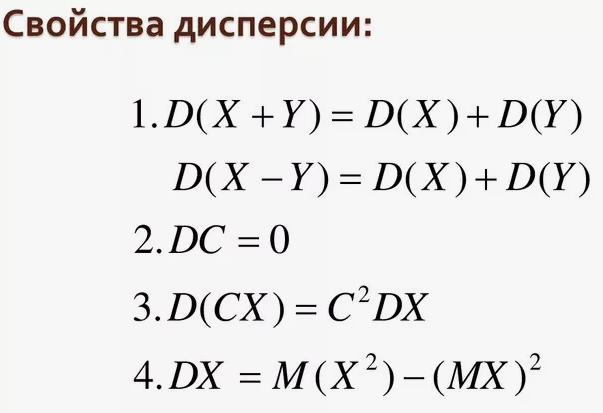


Записан рост (в сантиметрах) пяти учащихся: 158, 166, 134, 130, 132. На сколько отличается среднее арифметическое этого набора чисел от его медианы?
Решение:
1) Средн.арифм. = 158+166+134+130+132/5=144
2) 130 132 134 158 166 - расставляем в порядке возрастания, медиана = 134
3) 144-134=10 - разница между средн.арифм. и медианой
Ответ: 10.

На соревнованиях по математике стали известны результаты участников, показанные в баллах: 65, 78, 82, 70, 90, 78, 85, 88, 75, 82. Найдите: среднее арифметическое результатов, наибольшее и наименьшее значение баллов, размах, медиану, моду.
Ответ:
1. Среднее арифметическое:
(65+78 +82+70+90+78+85+88+75+82)/10 = 79.8
2. Наименьшее значение: 65, наибольшее значение: 90
3. Размах: 90 - 65 = 25
4. Медиана: 80 (после сортировки: 65,70,75,78,78,82,82,85,88,90 →
средние 78 и 82; (78+82)/2 = 80)
5. Мода: 78 и 82 (появляются чаще всего)
1) 134:100=1,34 – среднее арифметического старого набора
2) 1,34*101=135,34 – сумма всех чисел нового набора
3) 135,34-134=1,34 – это число добавили к набору
Ответ: 0,4
а) Построим вариационный ряд: 159, 169, 170, 174, 178, 184, 185, 189, 189, 191.
б) Объем ряда равен 10, размах ряда равен 42, мода ряда равна 189, медиана ряда равна 175.
в) Среднее арифметическое ряда равно 178,8.
Ответ: 189; 181; 178,8.

а) Облако данных очевидно наклонено вправо-вверх, что говорит о наличии возможной зависимости между ценой книги и количеством страниц.
б) На цену книги влияет качество бумаги, наличие иллюстраций, качество переплёта, число страниц, количество использованных цветов, покупательский спрос, талант автора и другие факторы.
в) Размах можно оценить в 250 рублей, если не учитывать выброс (книга, стоимостью более 600 рублей). Если его учитывать, то размах приблизительно равен 520 рублям.
