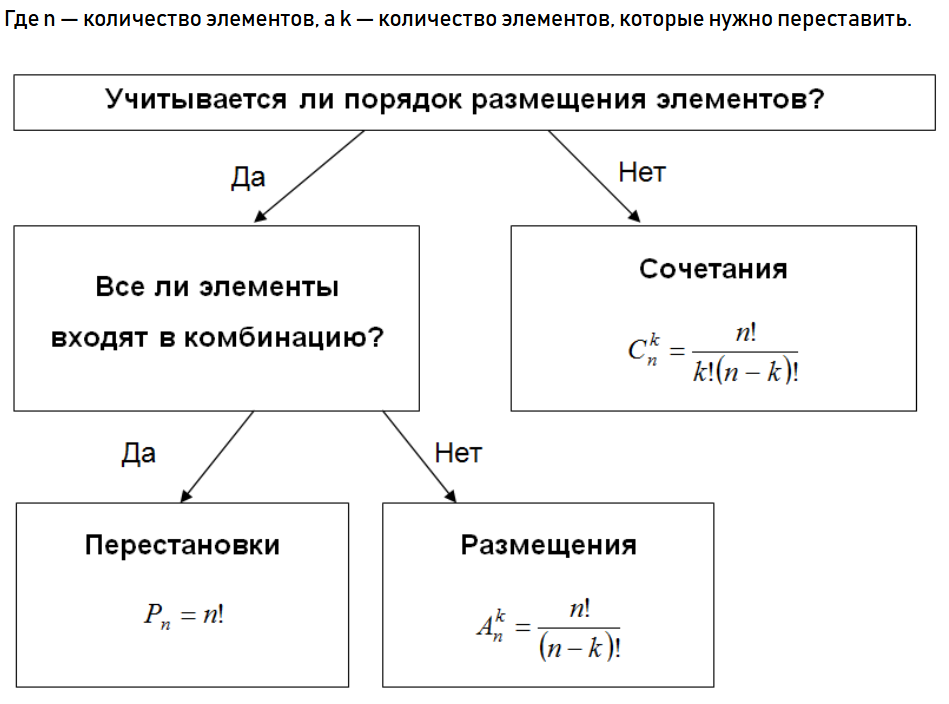
- Множество — набор элементов, которые перебирают.
- Выбор — действие, при котором из множества достают какие-то составляющие.
- Расположение — действие, при котором выбранные элементы расставляют в определённом порядке.
- Факториал — математическая функция, с помощью которой перемножают все числа от 1 до какого-то числа.
- Сложение — используется, когда выбирают элемент из нескольких пересекающихся подмножеств. Есть правило сложения: если элемент A можно выбрать n способами, и элемент B — m способами, то A или B можно выбрать n + m способами.
- Умножение — используется, когда выбирают элементы последовательно, друг за другом. Есть правило умножения: если элемент A можно выбрать n способами, а элемент B — m способами, то пару A и B можно выбрать n * m способами.
- Перестановка — это способ последовательно расположить составляющие множества. Например, 123, 312 и 213 — это перестановки трёх чисел: 1, 2 и 3.
- Сочетание — это набор элементов, который можно выбрать из множества без учёта порядка.
- Размещение — это упорядоченный набор элементов, который можно выбрать из множества.
ЭЛЕМЕНТЫ КОМБИНАТОРИКИ:
РАЗМЕЩЕНИЯ
Сочетание из n по k – это неупорядоченный набор из k различных элементов, взятых из некоторого множества
с мощностью n, где k ≤ n.
Операция сочетания помогает выяснить, сколькими способами можно выбрать k элементов из множества n.
В анализе данных сочетания позволяют, зная число комбинаций, вычислить вероятность, что открывает доступ к методам математической статистики: анализу данных и прогнозированию.
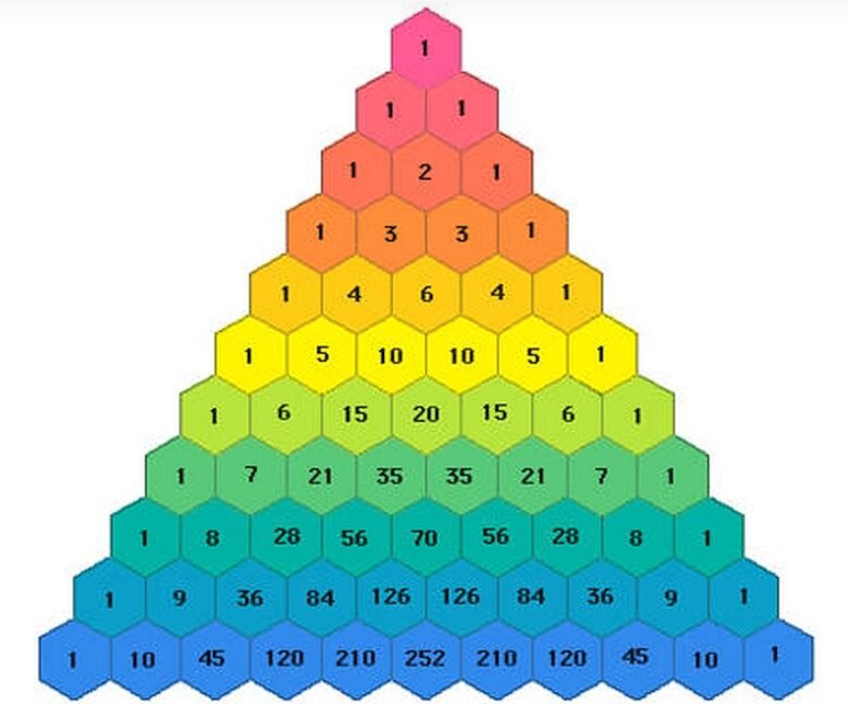
Треугольник Паскаля – это числовой треугольник, который содержит числа сочетаний. Его можно использовать, если количество элементов небольшое. Это бесконечная треугольная таблица, в которой на вершине и по боковым сторонам стоят единицы, а каждое из остальных чисел равно сумме двух чисел, стоящих над ним в предшествующей строке.

У мамы 2 яблока и 3 груши. Каждый день в течение 5 дней подряд она выдает по одному фрукту. Сколькими способами это может быть сделано?
Решение:
1) имеем набор {я, я, г, г, г}
2) всего перестановок пятиэлементного множества 5!, но мы не должны учитывать перестановки, в которых объекты одного типа меняются местами несколько раз, поэтому нужно поделить на возможное число таких перестановок: 2!*3!
3) получаем в итоге: 5/2!*3!=3*4*5/2*3 = 10
Ответ: 10 способов.

Сколько существует способов рассадить за круглый стол 5 юношей и 5 девушек так, чтобы они чередовались?
Решение:
1) предположим, что на месте номер 1 сидит юноша
тогда все юноши садятся через 1 от этого места (на нечетные места), а девушки – на четные
2) кол-во способов усадить 5 юношей на 5 кресел (кол-во перестановок) – это P5, кол-во способов усадить 5 девушек на 5 кресел – это также P5
3) следовательно, всего вариантов усадить юношей и девушек – это (P5)2, НО на месте номер 1 может сидеть девушка (на четных – юноши, на нечетных – девушки), тогда окончательный ответ будет в 2 раза больше, то есть 2*(P5)2
2*(P5)2=2*(5!)2
Ответ: 2*(5!)2 способов.



