СЛУЧАЙНАЯ ВЕЛИЧИНА И РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ
СЛУЧАЙНАЯ ВЕЛИЧИНА.
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ
ЗАКОН БОЛЬШИХ ЧИСЕЛ
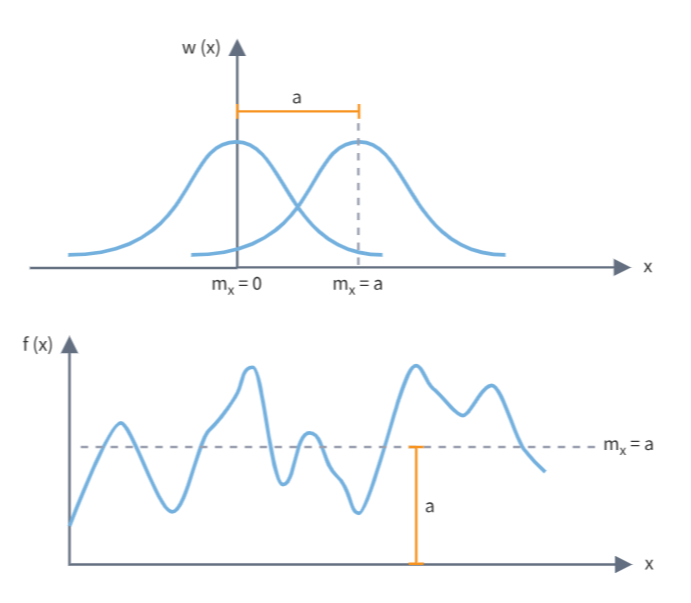
Закон больших чисел (ЗБЧ) – это принцип, описывающий результат выполнения одного и того же эксперимента много раз.
Согласно закону, среднее значение конечной выборки из фиксированного распределения близко к математическому ожиданию этого распределения. Другими словами, чем больше объём выборки, чем чаще проводятся измерения какого-либо параметра, тем выше вероятность того, что результаты окажутся близкими к ожидаемым.
В широком смысле под законом больших чисел понимается общий принцип, согласно которому совокупное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая. То есть при большом числе случайных величин их средняя величина перестаёт быть случайной и может быть предсказана с большой степенью определённости.
В узком смысле под законом больших чисел понимается ряд математических теорем, в каждой из которых для тех или иных условий устанавливается факт приближения средних характеристик большого числа опытов к определённым постоянным, неслучайным величинам.
Согласно закону, среднее значение конечной выборки из фиксированного распределения близко к математическому ожиданию этого распределения. Другими словами, чем больше объём выборки, чем чаще проводятся измерения какого-либо параметра, тем выше вероятность того, что результаты окажутся близкими к ожидаемым.
В широком смысле под законом больших чисел понимается общий принцип, согласно которому совокупное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая. То есть при большом числе случайных величин их средняя величина перестаёт быть случайной и может быть предсказана с большой степенью определённости.
В узком смысле под законом больших чисел понимается ряд математических теорем, в каждой из которых для тех или иных условий устанавливается факт приближения средних характеристик большого числа опытов к определённым постоянным, неслучайным величинам.
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ
Случайная величина – это величина, которая в результате опыта может принять одно из её возможных значений, но заранее неизвестно, какое именно. Это функция, которая сопоставляет каждому элементарному исходу случайного эксперимента числовое значение.
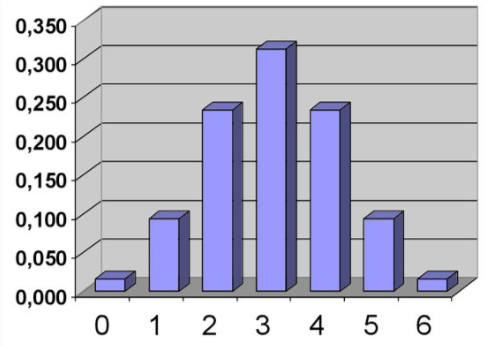
Распределение вероятностей – это закон, который каждому значению случайной величины ставит в соответствие вероятность того, что величина примет это значение.
Закон распределения случайной величины – это соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.
Распределение вероятностей можно задать таблицей, графиком, диаграммой, формулами или даже словесным описанием.
Основное свойство распределения – сумма всех вероятностей равна единице.
Распределение вероятностей – это закон, который каждому значению случайной величины ставит в соответствие вероятность того, что величина примет это значение.
Закон распределения случайной величины – это соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.
Распределение вероятностей можно задать таблицей, графиком, диаграммой, формулами или даже словесным описанием.
Основное свойство распределения – сумма всех вероятностей равна единице.
Математическое ожидание случайной величины – это её среднеожидаемое значение при многократном повторении испытаний.
Вычисляется как сумма значений этой случайной величины, умноженных на вероятности этих значений.
Некоторые свойства математического ожидания:
· Математическое ожидание постоянной величины равно самой постоянной величине.
· Постоянный множитель можно выносить за знак математического ожидания.
· Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий.
· Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий.
Если каждое значение случайной величины имеет одинаковую вероятность появления, то математическое ожидание можно определить как среднее арифметическое всех значений.
Вычисляется как сумма значений этой случайной величины, умноженных на вероятности этих значений.
Некоторые свойства математического ожидания:
· Математическое ожидание постоянной величины равно самой постоянной величине.
· Постоянный множитель можно выносить за знак математического ожидания.
· Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий.
· Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий.
Если каждое значение случайной величины имеет одинаковую вероятность появления, то математическое ожидание можно определить как среднее арифметическое всех значений.
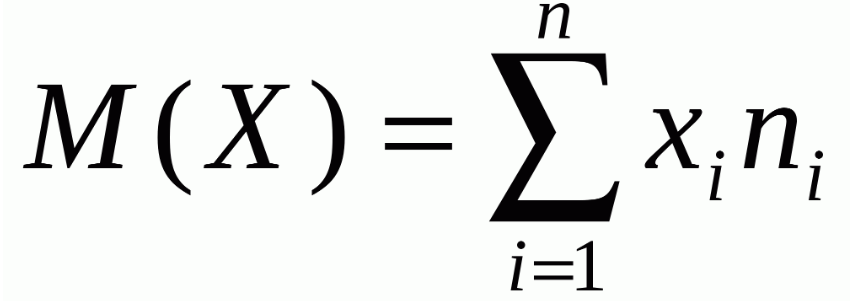


РЕШЕНИЕ ЗАДАЧ

Задача 1
В семье двое детей. Какова вероятность того, что оба ребёнка - девочки?
(М-мальчик, Д-девочка)
Решение:
1) возможные варианты: ММ, ДД, МД, ДМ
2) подходит только ДД (1 вариант)
3) p(А)=m/n=1/4=0,25, где А – событие рождения двух девочек, m – число благоприятных событий, n – число равновозможных событий
Ответ: 0,25.

Задача 2
Вычислить математическое ожидание дискретной случайной величины Х, заданной рядом:
xi | -1 | 2 | 5 | 10 | 20 |
pi | 0,1 | 0,2 | 0,3 | 0,3 | 0,1 |
Решение:
M(X)=Σni=1xi*pi = (-1)*0.1 + 2*0.2 + 5*0.3 + 10*0.3 + 20*0.1=6.8
Ответ: 6,8.
Решение:
1) т.к. вероятность попадания в корзину равна 0,7, значит, в среднем из 10 бросков будет 7 попаданий. Соответственно, из 50 бросков, будет в среднем 5*7=35 попаданий.
2) следовательно, математическое ожидание числа попаданий при 50 бросках равно 35.
Ответ: 35.
1) т.к. вероятность попадания в корзину равна 0,7, значит, в среднем из 10 бросков будет 7 попаданий. Соответственно, из 50 бросков, будет в среднем 5*7=35 попаданий.
2) следовательно, математическое ожидание числа попаданий при 50 бросках равно 35.
Ответ: 35.

Ответ: 3,5.

Ответ: -35.
